题目链接

[编程题]开根号

题面

在没有任何数学库函数的情况下，求一个数 m 开 n 次方的结果。

输入描述:

每组输入只有1行，包括有一个正实数m和一个正整数n，其中$1 <= n <= 32$, 1<=m<=$2^{n}$

输出描述:

输出只有一行，打印m开n次方的结果，小数点后面保留12位。

样例：

输入：
2 10
输出：
1.071773462536

解题过程

说点题外话，这个问题实际上就是要让我们手写幂函数的逻辑，因为一个有理数显然可以写成分数的形式，那么分子部分就是求整数幂，分母部分就是本题的开整数次方，所以最后就可以拼凑成 pow 函数的功能。

来自知乎回答：

标准库中，pow 的实现依赖于一种变形：$x=a^{\log_ax}$, a 一般都取自然常数 e ，即：$x=e^{\ln{x}}$。于是，$\sqrt[n]{x}$ 就等价于：$x^{\frac{1}{n}}=e^{\ln{x^{\frac{1}{n}}}}=e^{\frac{1}{n}*\ln{x}}$，这两部分就可以用泰勒级数取前 n 项逼近函数值了。

在数学课中，我们知道这种开根号求根问题，可以等价于它的反函数对应方程的解。比如这个问题的原问题是：
$$
y=\sqrt[n]{x},\ 当\ x=m\ 时，\ y\ 取何值？
$$
这个问题换个说法就是：
$$
x=y^n,\ 当\ x=m\ 时，\ y \ 取和值？
$$
这样看似在说废话，但是却有很多好处，因为我们可以枚举 $y$ 去找这个近似解了，当然我们可能还是不好枚举，因为这个 $y$ 可能是一个小数，这该怎么枚举呢？

随着这个枚举思路的引进，我们也看到了一点曙光，因为我们可以把解约束到某个长度为 1 的整数区间中了，这一步的做法是 $O(m)$ 的时间复杂度。但是要怎么更进一步提高解的精度呢？

我们观察，在线性的枚举过程中我们发现，这个枚举的序列其实是有序的，所以我们可以利用二分将上面的枚举优化到 $O(logm)$ 的时间复杂度。但这其实并不能提高解的精度，怎么办呢？

不难发现，其实这个长度为 1 的区间中，其实也是有序的，只不过他们是小数而已。于是，二分答案的算法呼之欲出。

二分答案

对于一个组询问，我们搜索区间 [0, m]，因为解一定存在，可以搜索到答案接近到一定精度后才结束搜索，所以二分的左端点和右端点类型应该是浮点数。当答案大于 m，选择左区间；否则选择右区间。算法时间复杂度 $O(logkm)$，k是某个常数。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <bits/stdc++.h>
using namespace std;
const double eps=1e-13;
long double n,m;
int main(){
    scanf("%llf%llf",&m,&n);
    long double l = 0.0, r = m;
    while(r - l >= eps || l - r >= eps) {
        long double mid = (r + l) / 2;
        long double tmp = mid;
        for (int i = 1; i < n; i++) tmp *= mid;
        if(tmp > m){
            r = mid;
        }else{
            l = mid;
        }
    }
    printf("%.12llf\n",l);
    return 0;
}

牛顿迭代法

我们知道牛顿迭代法可以求一些曲线零点，它的思想是用泰勒展开的前两项，也就是线性部分去逼近零点。已知二次根号比较容易做到了，那么 n 次根号实际上也是一样，只不过最后形成的式子稍微复杂一点。值得注意的是，计算机的浮点数会有精度误差，为了避免精度误差导致死循环等问题，除法要尽量少做。以下是推导过程：

设 $y=x^n-m$，则 $y’=nx^{n-1}$。
牛顿迭代法
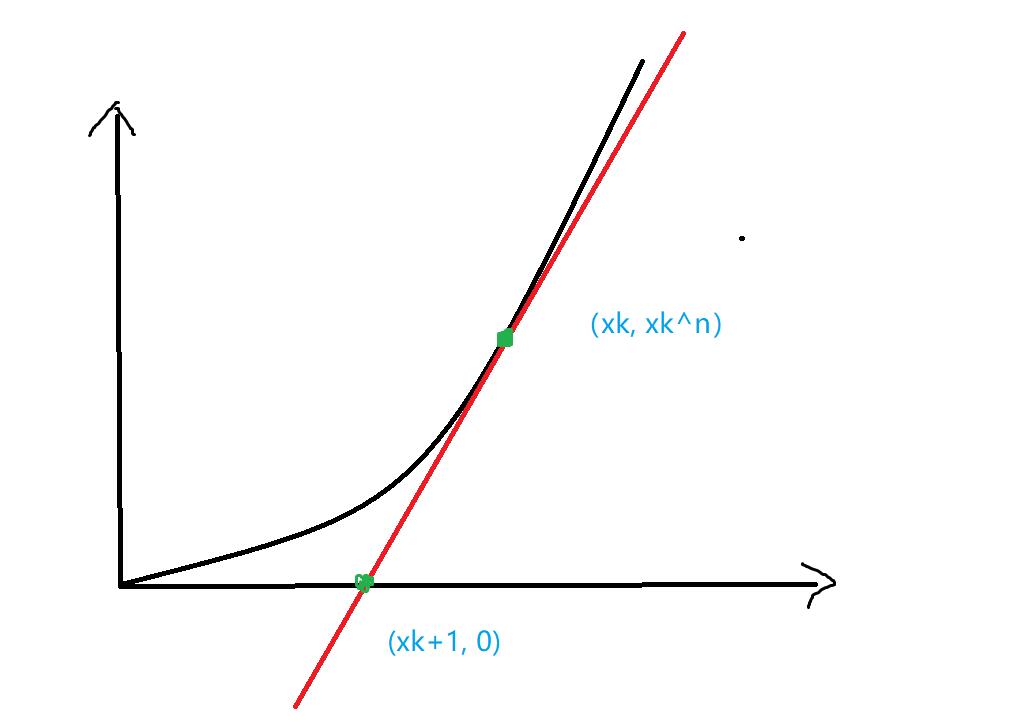
实际上，牛顿迭代法就是在当前点求切线，利用切线和 x 轴的交点跳到那个交点横坐标所对应的曲线位置，迭代后逼近曲线的零点。于是，利用导函数和切线我们可以得到以下式子：
$$
斜率k=\frac{0-({x_k}^n-m)}{x_{k+1}-x_k}=n{x_k}^{n-1} \iff x_{k+1}=x_k-\frac{x_k}{n}+\frac{m}{n}{x_k}^{1-n}
$$
于是，利用这个式子，我们不断迭代使得第 k 项和第 k + 1 项接近到一定精度即可。（注意这边区别于二分的做法就是不用再去考虑根的 n 次方接近 m 的精度，因为两者是几乎等价的）。

注意做 ${x_k}^{1-n}$ 这项尽量先用乘法做 n - 1 项，然后再做一次除法，避免精度误差。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <bits/stdc++.h>
using namespace std;
const long double esp = 1e-13;
int n;
long double m, xk1, xk, cur, tmp;

int main(){
    scanf("%llf%d",&m, &n);
    cur = m;
    do {
        xk = cur;
        xk1 = xk;
        tmp = n / m;
        for (int i = 1; i < n; i++) tmp *= xk;
        xk1 += 1.0 / tmp - xk / n;
        cur = xk1;
    }while(xk - xk1 >= esp || xk1 - xk >= esp);
    printf("%.12llf\n", xk1);
    return 0;
}